Виды моделирования. Графическое моделирование как основное средство

Как найдем на сколько больше красных шаров? (Нужно из красных отодвинуть столько, сколько синих, узнаем на сколько больше красных шаров).

Какое действие выберем? (Мы отодвинули шары, значит, действие «вычитание»).

6-4=2 (ш).

?

Учим правило «Чтобы сравнить, на сколько одно число больше другого, нужно из большего числа вычесть меньшее».

Итак, целенаправленная работа по формированию приемов умственной деятельности начинается с первых уроков математики при изучении темы “Отношения равенства-неравенства величин”. Действуя с различными предметами, пытаясь заменить один предмет другим, подходящим по заданному признаку, дети выделяют параметры вещей, являющиеся величинами, т.е. свойства, для которых можно установить отношения равно, неравно, больше, меньше. В контексте задач дети знакомятся с длиной, массой, площадью, объемом. Полученные отношения моделируются сначала с помощью предметов, графически (отрезками), а затем - буквенными формулами.

На первых же уроках нужно познакомить детей с прямой и кривой линией, а затем с понятием отрезка и научить чертить отрезки по линейке. Для этого можно выполнить упражнение следующего вида:

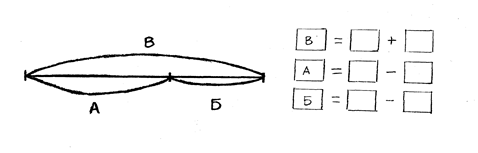
После того как дети хорошо разберутся в понятии “задача”, можно учить их составлять задачи по картинкам, причем все виды задач. Здесь полезно применять чертежи и схематические рисунки, блок-схемы, моделирование с помощью отрезков, таблиц и матриц.

Графические модели и таблицы позволяют сравнивать пары понятий: левая – правая, верхняя – нижняя, увязывать пространственную информацию (правая – левая) с информацией меры (широкая - узкая, короткая - длинная) тем самым формируя умение решать задачи. Примером может служить таблица:

В беседе со школьниками по этой матрице следует задавать противопо-ложные по содержанию вопросы.

Вопрос: какая лента нарисована в правой нижней клетке? Ответ: длинная и узкая. Вопрос: где нарисована короткая и широкая лента? Ответ: в левой верхней клетке.

Табличные примеры удобны для быстрого решения примеров, информационно связанных друг с другом (рис.3). Так, например, заполняя клетки таблицы, школьники должы обратить внимание на совпадение парных сумм, например: 35+47=45+37=82.

Статьи по педагогике:

Анализ состояния функционального базиса письма у старших дошкольников с нарушением речи
Письмо и чтение представляют собой особые формы речевой деятельности, имеющие сложную психологическую структуру. Формирование навыков письма и чтения тесно связано с развитием устной речи. Поэтому при недоразвитии устной речи возникает необходимость обследовать не только уровень развития языковых с ...

Методика развития техники чтения на уроках литературного чтения
Результаты диагностики уровня навыка чтения и читательского кругозора дали нам возможность проектировать эффективную для данного класса систему коррекционной работы по овладению навыком чтения с использованием творческих упражнений. Анализ методической литературы позволил выделить следующие упражне ...

Характеристика комплекса дидактических игр по развитию речевой деятельности у детей старшего дошкольного возраста
Мы изучили много различных дидактических игр различной вариативности предлагаемых Бондаренко А.К., а также Швайко Г.С. опираясь на разработки этих авторов, мы создали комплексы дидактических игр из игр разных разделов развития речевой деятельности: - расширение ориентировки в окружающем и формирова ...