Определение золотого сечения

Покровительство Фридриха и стимулировало выпуск научных трактатов Фибоначчи:

книга абака, написанная в 1202 году, но дошедшая до нас во втором своем варианте, который относится к 1228 г.

практики геометрии (1220г.)

книга квадратов (1225г.)

По этим книгам, превосходящим по своему уровню арабские и средневековые европейские сочинения, учили математику, чуть ли не до времен Декарта(XVII в.).

Наибольший интерес представляет для нас сочинение "Книга абака". Эта книга представляет собой объемный труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший значительную роль в развитии математики в Западной Европе в течение нескольких следующих столетий.

Сообщаемый в "Книге абака" материал поясняется на примерах задач, составляющих значительную часть этого тракта.

Как сказано выше, золотая пропорция тесно связана с последовательностью Фибоначчи. А началось всё с того, что Кеплер, спустя четыре столетия после открытия этого ряда установил, что отношение рядом стоящих чисел в пределе стремится к золотой пропорции Ф. Это свойство присуще не только числам Фибоначчи. Начав с любых двух чисел, и построив аддитивный ряд, в котором каждый член равен сумме двух предыдущих (например, ряд 7,2,9,11,20…), мы обнаружим, что отношение двух последовательных членов такого ряда так же стремится к числу Ф: чем дальше будем продвигаться от начала ряда, тем лучше будет приближение.

На страницах 123 - 124 данной рукописи, Фибоначчи поместил следующую задачу:

Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет др. пару, а рождают кролики со второго месяца после своего рождения.

Ясно, что если считать первую пару кроликов новорожденными, то на второй месяц мы будем по прежнему иметь одну пару; на 3-й месяц- 1 + 1 = 2; на 4-й- 2 + 1 = 3 пары (ибо из двух имеющихся пар потомство дает лишь одна пара); на 5-й месяц – 3 + 2 = 5 пар (лишь 2 родившиеся на 3-й месяц пары дадут потомство на 5-й месяц); на 6-й месяц – 5 + 3 = 8 пар (ибо потомство дадут только те пары, которые родились на 4-м месяце) и т. д.

Выглядит это так.

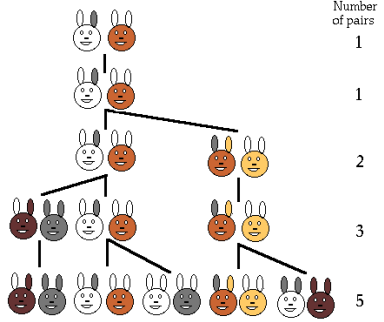
И так далее.

Таким образом, если обозначить число пар кроликов, имеющихся на n-м месяце через Fк, то F1=1, F2=1, F3=2, F4=3, F5=5, F6=8, F7=13, F8=21 и т. д., причем образование этих чисел регулируется общим законом: Fn=Fn-1 + Fn-2

При всех n > 2, ведь число пар кроликов на n-м месяце равно числу Fn-1 пар кроликов на предшествующем месяце плюс число вновь родившихся пар, которое совпадает с числом Fn-2 пар кроликов, родившихся на (n-2)-ом месяце (ибо лишь эти пары кроликов дают потомство).

Числа Fn, образующие последовательность 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, . называются "числами Фибоначчи", а сама последовательность - последовательностью Фибоначчи.

Суть последовательности Фибоначчи в том, что, начиная с 1, 1 следующее число получается сложением двух предыдущих.

Но почему эта последовательность так важна?

Данная последовательность асимптотически (приближаясь, все медленнее и медленнее) стремится к некоторому постоянному соотношению. Однако, это соотношение иррационально, то есть представляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно.

Если какой-либо член последовательности Фибоначчи разделить на предшествующий ему (например, 13:8), результатом будет величина, колеблющаяся около иррационального значения 1.61803398875 .и через раз то превосходящая, то не достигающая его. Но, даже затратив на это Вечность, невозможно узнать соотношение точно, до последней десятичной цифры. Краткости ради, мы будем приводить его в виде 1,618.

Особые названия этому соотношению начали давать еще до того, как Лука Пачоли (средневековый математик) назвал его Божественной пропорцией. Среди его современных названий есть такие, как Золотое сечение, Золотое среднее и отношение вертящихся квадратов. Кеплер назвал это соотношение одним из "сокровищ геометрии". В алгебре общепринято его обозначение греческой буквой фи. Ф = 1,618

Асимптотическое поведение последовательности, затухающие колебания ее соотношения около иррационального числа Ф могут стать более понятными, если показать отношения нескольких первых членов последовательности. В этом примере приведены отношения второго члена к первому, третьего ко второму, четвертого к третьему, и так далее:

1:1 = 1.0000, что меньше ф на 0.6180;

2:1 = 2.0000, что больше ф на 0.3820;

3:2 = 1.5000, что меньше ф на 0.1180;

5:3 = 1.6667, что больше ф на 0.0486;

8:5 = 1.6000, что меньше ф на 0.0180;

Статьи по педагогике:

План занятий математического кружка учащихся 6-х классов и методические рекомендации к ним
Содержание занятий разработано из расчета одно занятие в две недели, что составляет 18 занятий за учебный год. План занятий математического кружка учащихся 6-х классов: задачи на делимость; признаки делимости на 3 и на 9; признаки делимости на 7, на 11, на 13; прямая и обратная пропорциональность; ...

Сущность и основные понятия дистанционного обучения
Последние 10 лет все более проявляется развитие информационных технологий во многих отраслях человеческой деятельности. Интернет становится едва ли не основным средством обмена информацией и приобретает все большую популярность. Кроме того, развитие IT-технологий обуславливает их использование в са ...

Особенности трудового воспитания детей с недостатками слуха
Труд является исторически первичным видом человеческой деятельности и составляет основу для развития человека в филогенезе и онтогенезе. В процессе труда человек не только осуществляет воздействие на окружающую действительность, но и активно изменяет свою собственную природу. Задачи трудового воспи ...