Определение золотого сечения

Иоганн Кеплер говорил, что геометрия владеет двумя сокровищами - теоремой Пифагора и золотым сечением. И если первое из этих двух сокровищ можно сравнить с мерой золота, то второе с драгоценным камнем.

Теорему Пифагора знает каждый школьник, а что такое золотое сечение – далеко не все.

Пропорция – равенство между двумя отношениями четырёх величин: a:b=c:d. Возьмём пример, предлагаемый Васютинским, где АВ, который можно разделить на две равные части №1. Это будет соотношение разных величин – АВ : АС=АВ : ВС. Эту же прямую №2 и №3 можно разделить на две неравные части в любом отношении. Эти части пропорции не образуют. А вот прямую АВ №4 можно разделить по золотому сечению, когда АВ: АС, как АВ : ВС. Это и будет искомым золотым сечением (золотым делением) или деление в крайнем и среднем отношении.

Рис. 3. Деление отрезка прямой на равные части и по золотому сечению:

№1 – АВ : АС;

№2, №3 – пропорция не образуется;

№4 – АВ : АС = АС : ВС или ВС : АС = АС : АВ (золотая пропорция)

Золотое сечение – это такое пропорциональное гармоническое деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей. Или другими словами, меньший отрезок относится к большему, как больший ко всему, т.е. а:в=в:с или с:в=в:а.

Определение в крайнем и среднем отношении становится более понятно, если выразить его геометрически. На рисунке 4 приведено геометрическое изображение золотой пропорции.

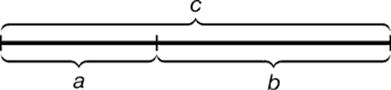
Рис. 4, а

Рис. 4, б

Отрезки золотой пропорции, если их, конечно, продолжат (рис. 4,б) дальше, выражаются иррациональной бесконечной дробью 0,618 ., если с принять за единицу, а = 0,382.…На этой пропорции базируются основные геометрические фигуры.

Прямоугольник с таким отношением сторон стали называть золотым прямоугольником. Он также обладает интересными свойствами. Если от него отрезать квадрат, то останется вновь золотой прямоугольник. Этот процесс можно продолжать до бесконечности. А если провести диагональ первого и второго прямоугольника, то точка их пересечения будет принадлежать всем получаемым золотым прямоугольникам.

Разумеется, существует и золотой треугольник. Это равнобедренный треугольник, у которого отношение длины боковой стороны к длине основания равно числу Ф (с ним мы встретимся в разделе золотые фигуры).

Астроном Иоганн Кеплер называл эту последовательность продолжающей саму себя. «Устроена она так, - писал Кеплер, - что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причём та же пропорция сохраняется до бесконечности».

Как можно заметить, построение ряда отрезков золотой пропорции можно производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд).

Практическое знакомство с золотым сечением, как правило, начинается с деления отрезка прямой в золотой пропорции геометрическим способом (рис. 5).

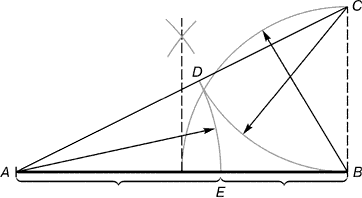
Рис. 5

Из точки. В восстанавливаем перпендикуляр, равный половин АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок равный ВС, заканчивающийся точкой D. Отрезок АD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.

В этом случае геометрическую пропорцию можно выразить следующим образом:

Где АД = х.

Если АВ = а принять за единичный отрезок, то получим следующее числовое выражение:

будем обозначать Ф. при этом

Обратим внимание удивительную инвариантность золотой пропорции:

Такие преобразования как возведение в степень не смогли уничтожить сущность этой уникальной пропорции.

Подобно числу π, Ф можно представить в виде суммы бесконечного ряда многими способами. Одно из них:

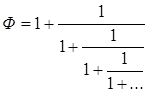
1.3 Открытие Леонардо Фибоначчи

Итальянский купец Леонардо из Пизы (1180-1240), более известный под прозвищем Фибоначчи был, безусловно, самым значительным математиком средневековья. Роль его книг в развитии математики и распространении в Европе математических знаний трудно переоценить.

Жизнь и научная карьера Леонардо теснейшим образом связана с развитием европейской культуры и науки.

В век Фибоначчи возрождение было еще далеко, однако история даровала Италии краткий промежуток времени, который вполне можно было назвать репетицией надвигающейся эпохи Ренессанса. Этой репетицией руководил Фридрих II, император (с 1220 года) Священной Римской империи.

Статьи по педагогике:

Формы, особенности методов обучения по дисциплине «Природопользование»
Форма обучения по дисциплине «Природопользование» может быть как очной (дневной), так и заочной. При изучении учебной дисциплины «Природопользование» обращается внимание студентов СУЗов на ее прикладной характер, где и когда изучаемые теоретические положения и практические умения могут быть использ ...

Педагогический идеал и его конкретно-историческое воплощение
Человек, которого должно сформировать в нас воспитание, - это не тот человек, которого создала природа, а тот, каким его хочет видеть общество, а оно его хочет видеть таким, каким требует экономика этого общества. Доказательством этого служит то, как менялось наше представление о человеке в зависим ...

Учебная деятельность студентов и физическое воспитание
Известно, что учебная деятельность студентов - это 36 часов академических занятий в неделю. Проходят они, за исключением уроков физкультуры, в аудиториях и лабораториях, не всегда соответствующих гигиеническим нормам. Обязательным продолжением академических занятий является самостоятельная работа с ...