Золотые фигуры

Отрезки золотой пропорции выражаются иррациональной бесконечной дробью 0,618 ., если с принять за единицу.

а = 0,382…как мы уже знаем числа 0.618 и 0.382 являются коэффициентами последовательности Фибоначчи. На этой пропорции базируются основные геометрические фигуры.

Построение золотого прямоугольника:

Если построить квадрат со стороной АВ (рис. 6), найти середину М отрезка АВ и провести дугу окружности радиусом МС с центром в точке М до пересечения с продолжением стороны АВ в точки Е, то точка. В разделит отрезок АЕ в среднем и крайнем отношении.

Рис. 6

Рассматривая золотой прямоугольник можно заметить что, если отрезать от него квадрат, сторона которого равна меньшей стороне прямоугольника, то мы снова получим золотой прямоугольник меньших размеров. И если продолжать в таком порядке, то получим совершенно квадратируемый прямоугольник бесконечного порядка. Точки, делящие стороны прямоугольника в среднем и крайнем отношении, лежат на логарифмической спирали, закручивающейся вовнутрь. Полюс спиралей лежит на пунктирных диагоналях (рис. 7).

| | 0.500 | 0.618 |

Рис. 7, а. Золотая спираль

Рис. 7, б. Спираль Фибоначчи.

Спираль золотого сечения закручивается в бесконечность. Но есть ещё одна спираль, спираль Фибоначчи. Она построена из шести квадратов одного размера («конечна»). Возьмём раковину моллюска наутилуса: «Существует неписаное правило, что в любой хорошей книги по сакральной геометрии должна быть раковина нотариуса. Во многих книгах сказано, что это спираль золотого сечения, но это не верно – это спираль Фибоначчи. Можно увидеть совершенства рукавов спирали, но если посмотреть на центр и начало, то он не выглядит таким совершенным. Советую вам увидеть настоящую раковину. Два первых внутренних изгиба фактически равны, и отношение их дли равно 1, что далеко от фи. Второй и третий виток всё ближе и ближе приближается к 1,618. Потом получается эта изящная спираль. Можно подумать, что этот маленький моллюск в самом начале; похоже, он не ведал, что творил. Нет, он творит прекрасно, это не ошибка. Просто он чётко следует математике ряда Фибоначчи» (Друнвало Мелхиседек).

Эта спираль возникает и в других геометрических построениях. Возьмём золотой треугольник, стороны которого находятся в золотом отношении к основанию. Этот треугольник будет равнобедренный (Рис. 8), у которого отношение длины боковой стороны к длине основания равняется 1,618 (приложение 1). Углы при основании такого треугольника равны по 72о, что вдвое больше угла при вершине, равного 36о. Точка пересечения биссектрисы угла при основании с противоположной стороной делит эту сторону в среднем и крайнем отношении, при этом весь треугольник разбивается на два меньших, один из которых подобен исходному. Так же и этот треугольник можно разбить на более мелкие. Продолжая это, получим бесконечную последовательность закручивающихся треугольников (логарифмическую).

Логарифмическая спираль – единственный тип спирали, не меняющей своей формы при увеличении размеров.

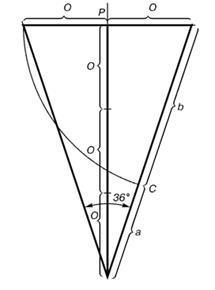
Рис. 9. Золотой треугольник

Есть и золотой кубоид – это прямоугольный параллелепипед с ребрами, имеющими длины 1.618, 1 и 0.618.

В звездчатом пятиугольнике каждая из пяти линий, составляющих эту фигуру, делит другую в отношении золотого сечения, а концы звезды являются золотыми треугольниками.

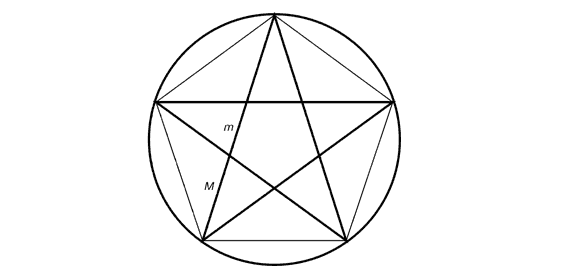
Рис. 9. Построение правильного пятиугольника и пентаграммы (пентакл)

Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и служила опознавательным знаком. Бытует легенда о том, что один из пифагорейцев больным попал в дом к незнакомым людям. Они старались его выходить, но болезнь не отступала. Не имея средств заплатить за лечение и уход, больной перед смертью попросил хозяина дома нарисовать у входа пятиконечную звезду, объяснив, что по этому знаку найдутся люди, которые вознаградят его. И на самом деле, через некоторое время один из путешествующих пифагорейцев заметил звезду и стал расспрашивать хозяина о том, каким образом она появилась у входа. После рассказа хозяина гость щедро вознаградил его. Пентаграмма была хорошо известна и в Древнем Египте. Но непосредственно как эмблема здоровья она была принята лишь в Древней Греции.

Статьи по педагогике:

Классификация наглядных методов
Сущность метода иллюстрации и демонстрации заключается в наглядном представлении (показе) учащимся натуральных предметов, явлений, процессов или их макетов, моделей и изображений в зависимости от конкретных учебно-воспитательных задач. В отдельных случаях демонстрация предполагает постановку опытов ...

Преступность как форма проявления делинквентного поведения детей и подростков
Преступность несовершеннолетних и молодежи во всем мире является одной из самых актуальных социальных проблем. Рост такой преступности характерен для всех развитых стран мира. К основным причинам преступности несовершеннолетних и молодежи ученые отно­сят безработицу среди молодежи, неуверенность мо ...

Методы дистанционного университетского образования
Важным интегрированным фактором типологии дистанционных университетов является совокупность используемых в учебном процессе педагогических методов и приемов. Выбрав в качестве критерия способ коммуникации преподавателей и обучаемых, эти методы (приемы) можно классифицировать следующим образом: 1)Ме ...