Обучение решению задач на движение с помощью схематического моделирования

На подготовительном этапе на основе движущихся моделей дети должны уяснить что значит двигаться навстречу друг другу и в противоположных направлениях. Необходимо познакомить детей с элементами чертежей к задачам на движение и научить их вычерчивать по условию задачи.

24 м ?, на 8 м <

? м

После такого предварительного знакомства вводится понятие "скорость". Беседа начинается с того, что есть предметы движущиеся и не движущиеся (дети приводят примеры). Опираясь на жизненный опыт детей, выясняем, что одни предметы движутся быстрее, другие медленнее.

Открываем таблицу на доске:

В этом случае говорят, что скорость пешехода 5 км в час (показываем запись 5 км/ч) и т. д.

Скорость движения — это расстояние, которое проходит движущийся предмет за единицу времени (за 1 час, за 1 минуту, за 1 секунду).

- Проверим, как вы меня поняли. Скорость поезда 70 км/ч. Что это означает? (Поезд проезжает 70 км за 1 час.)

- Скорость мухи — 5 м/с — ?

- Скорость африканского страуса — 120 км/ч — ?

Задача. Велосипедист был в пути 3 ч и проехал за это время 36 км. В течение каждого часа он проезжал одинаковое расстояние. Сколько километров проезжал велосипедист в каждый час?

36 ч

Пояснить, что чёрточки означают количество часов.

36 : 3 = 12 (?)

Мы нашли, сколько километров проезжал велосипедист за каждый час, т. е. за 1 час или за единицу времени. Что же это за величина? (Скорость.) Как обозначим единицу измерения скорости? (км/ч)

36 : 3 = 12 (км/ч) V = S : t

скор .расст. вр.

Вывешивается формула и заучивается правило. На следующих уроках вводятся два других правила. После того, как дети выучат правила, задачи решаются в два и более действия; используется краткая запись в виде чертежа или таблицы.

Необходимо познакомить детей с понятием "общей скорости" (скорость сближения или удаления) и пояснить, что использование понятия "общая скорость" упрощает решение задач.

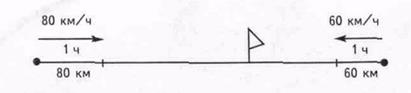
рис.2.

60 + 80 = 140 (км/ч) — общая скорость. На 140 км сблизятся машины за 1 час.

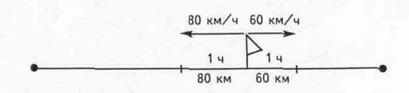
На 140 км удалились машины друг от друга за 1 час.

Чтобы дети уяснили решение задач через "общую скорость", нужно первые задачи разобрать от данных к вопросу.

— Известно "общее" расстояние 390 км и известно время — 3 ч. Что можно найти, зная расстояние и время?

— Если дано "общее" расстояние, то какую скорость мы найдём? (Найдём общую скорость.)

— Теперь, зная "общую скорость" и скорость первого автомобиля, что можно найти? (Скорость второго автомобиля.)

— Ответили мы на вопрос задачи? (Да.)

Весьма поучительно решение следующей четверки задач, исчерпывающих все возможные комбинации направлений движения двух тел относительно друг друга (рис.7). Вопрос для всех задач общий: через сколько секунд А и В окажутся рядом? Итак, дана задача: «Между двумя точками А и В имеются две дороги, длинная — 160 м и короткая — 80 м. Из этих точек движутся два велосипедиста со скоростями 5 и 3 м в секунду. Через сколько секунд они окажутся рядом? (Рассмотреть все возможные случаи.)»

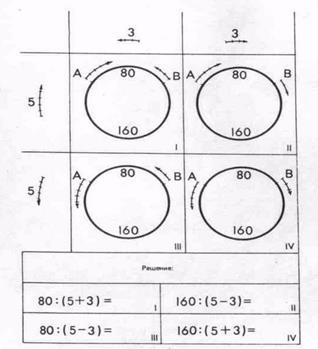
Решение задачи удобно изобразить в матрице с двумя входами.

Подобная четверка задач позволяет рассмотреть исчерпывающим образом математическую ситуацию, перебирая все возможные сочетания направлений движения двух тел. При таком оформлении четверки задач информация о направлении движения передается на нескольких кодах: по горизонтальному входу матрицы показаны скорости велосипедиста А, по вертикальному входу матрицы показаны скорости велосипедиста В. Эти же скорости изображены и на самих рисунках в матрице. По этой схеме удобно проводить обучающую беседу, позволяющую добыть дополнительную информацию об изучаемом.

Вопрос. В каких клетках изображено движение в противоположных направлениях (навстречу»)? Ответ. Движение «навстречу» изображено в клетках правой диагонали (I и IV). Вопрос. В каких клетках изображено движение в одном направлении («вдогонку»)? Ответ. Движение вдогонку изображено в клетках левой диагонали (11 и III). Вопрос. Сравните задачи (II и III). В каком случае быстрее нагонит один велосипедист другого? Почему? Ответ. В первом случае, так как в этом случае первоначальное расстояние между велосипедистами – 80 м. во втором случае – больше (160 м).

Статьи по педагогике:

Анализ уровня обучаемости учащихся лицея
Проводя исследования учащихся, поступающих в образовательное учреждение начального профессионального образования для получения специальности, педагоги Качканарского технического лицея детально анализируют начальный уровень развития ученика с помощью входной диагностики. Одним из направлений являетс ...

Исследование физико-географических условий Северного морского пути
Льды являются единственным препятствием для признания Северного морского пути – путем обычного нормального плавания. Толщина однолетних льдов 0,8–1,8 м, многолетних 3–4 м. Торосы обычно имеют высоту 3–5 м, в отд. случаях до 10–15 м. Встречаются айсберги и ледяные острова – оторвавшиеся участки шель ...

Третий этап эксперимента. Обследование устной речи глухих школьников после проведения серии экспериментальных занятий
На данном этапе мы выяснили результаты проведенных экспериментальных занятий, насколько они были полезными и к каким изменениям привели. В контрольном эксперименте использовались те же методики обследования речи испытуемых, что и в констатирующем эксперименте. Кроме того, весь речевой материал, исп ...