План занятий математического кружка учащихся 6-х классов и методические рекомендации к ним

На следующих занятиях рассматриваются недесятичные позиционные системы счисления на примере двоичной. Объяснение опирается на исторический и занимательный материал. Для первичного закрепления выполняются задания на перевод чисел из десятичной системы счисления в двоичную и обратно. Вводятся действия сложения и вычитания в двоичной системе счисления. Целесообразно дать возможность учащимся самостоятельно сформулировать правила выполнения этих действий в двоичной системе счисления, по аналогии с десятичной системой счисления. Такое задание можно дать предварительно в качестве домашнего и на занятии разобрать полученные дома результаты, решить несколько примеров на сложение и вычитание в двоичной системе счисления.

При изучении темы «Двоичная система счисления; Действия в двоичной системе счисления» можно предложить следующий способ отгадывания задуманного числа по спичкам: загадавший число мысленно делит его пополам, полученную половину еще раз пополам и т.д (отбрасывая от нечетного числа единицу) – и при каждом делении кладет на стол спичку вертикально, если число четное, и горизонтально, если оно нечетное.

Таким образом, получается некоторая фигура (рис. 1). Посмотрев внимательно на полученную фигуру, вы безошибочно определяете задуманное число. На данном рисунке изображено число 137. Такой рисунок представляет собой закодированную информацию в двоичной системе счисления (рис. 2).

Рис. 1.

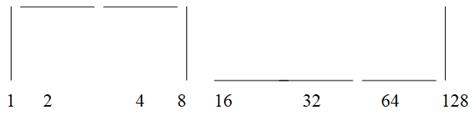
Рис. 2.

Вертикальная спичка соответствует 1, а горизонтальная – 0. Остается сложить соответствующие степени двойки. В данном примере имеем: 128+8+1=137. Это и есть задуманное число.

На занятии сначала учитель предлагает учащимся определить, какое число было задумано, если получились схемы (рис. 3, 4).

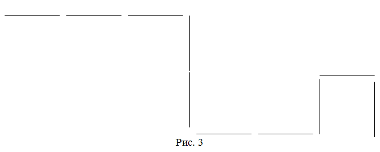
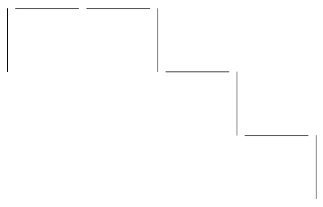
Рис. 4

А затем учащиеся разбиваются на группы по два и составляют аналогичные задания друг для друга. Можно организовать конкурс на лучшего кодировщика, определив, кто за определенное время лучше всего может отгадывать числа по схеме и наоборот кодировать задуманное число.

Это обучающая, качественная, одиночная, познавательная игра, можно ее провести и как игру – соревнование.

Далее учащиеся знакомятся с действиями умножения и деления в недесятичных системах счисления. Сначала преподаватель объясняет, как выполняются действия в двоичной системе счисления, а затем на примере систем с основанием 3 и 5 учащиеся знакомятся с умножением и делением в других системах счисления. В зависимости от подготовки кружковцев, учитель может предложить им составить таблицы умножения для других систем счисления и самостоятельно вывести правила, по которым выполняются вышеуказанные действия.

При рассмотрении темы «Различные системы счисления» учащимся можно предложить следующее творческое задание:

Учитель в процессе объяснения нового материала предлагает следующую задачу. В бумагах одного чудака – математика найдена была его автобиография. Она начиналась следующими строками: «Я окончил курс университета 44 лет отроду. Спустя год, 100 летним молодым человеком, я женился на 34 летней девушке. Незначительная разница в возрасте - всего 11 лет – способствовала тому, что мы жили общими интересами и мечтами. Спустя немного лет у меня была уже и маленькая семья из 10 детей. Жалования я получал в месяц всего 200 рублей, из которых десятую часть приходилось отдавать сестре, так что мы с детьми жили на 130 рублей в месяц».

Далее перед учащимися ставится вопрос: чем можно объяснить странные противоречия в числах этого отрывка? Ребята определяют, что единственная причина кажущегося противоречия заключается в том, что все числа, используемые чудаком – математиком, изображены в недесятичной системе счисления.

Возникает проблема: о какой именно системе счисления идет речь, то есть чему равно основание данной системы?

Если учащиеся не могут сами найти секрет, то необходимо с помощью вопросов направить их поиски к отысканию разгадки, которая заключается во фразе: «спустя год (после 44 лет) 100-летним молодым человеком…». Так как от прибавления единици число 44 преображается в 100, значит, цифра 4 – наибольшая цифра в этой системе, следоватнльно, основанием системы является 5.

После проведенной работы на занятии формулируется задание (оно может быть домашним): составить историю с использованием чисел, записанных в недесятичной системе счисления. Необходимо пояснить, что сюжет историй может быть самым разнообразным, но в тексте должна обязательно содержаться информация, в которой заключен ключ к определению основания системы счисления.

Статьи по педагогике:

Психофизиологические процессы при работе с компьютером
Исследование взаимодействия «Человек – компьютер» является сравнительно новым направлением. Это связано с тем, что компьютерной революции еще не более сорока лет. Компьютеризация образования, по мнению Н.И. Даниловой, создает «наиболее благоприятные условия для контроля обучения по физиологическим ...

Система мероприятий для формирования волевых качеств учащихся
Итак, на основе теоретического исследования психологии детского характера и стиля педагогического общения, мы определили, что самым оптимальным стилем общения является демократический стиль и стиль, где общение и деятельность строятся на творческом сотрудничестве. Этот стиль характеризуется положит ...

Изучение культуры Средневековой Европы в школе
Цель изучения раздела – знакомство учащихся с характерными особенностями культуры Средневековой Европы, формирование целостного представления об искусстве и мировоззрении средневекового человека. Задачи: познакомить учащихся с характерными чертами культуры средневековой Европы; развить творческое м ...