Психолого-педагогические особенности учащихся гуманитарных классов

Но для этого надо найти хотя бы один отрезок. Попробуем отыскать больший отрезок. Допустим, что сначала речь пойдёт не о построении отрезка, а о нахождении его длины. Этот вопрос (задача) будет решаться приблизительно так: если длину всего отрезка обозначим за а, а длину большей части х, то длина другой части будет равна а – х, то есть

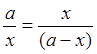
Отсюда, х2 = а(а – х) или х2 + ах – а2 = 0

Решив уравнение, получим

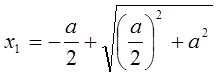
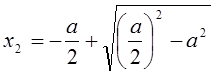
Возьмём положительный корень уравнения:

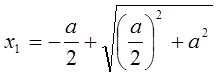
Получим

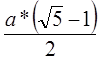
Таким образом, задача всегда имеет единственное решение.

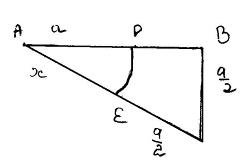
Исходя из теоремы Пифагора, то выражение, находящееся под корнем можно расценивать как гипотенузу треугольника с катетами равными а и а/2, тогда х – разность между гипотенузой и а/2, то есть что бы разделить отрезок в заданном отношении, нужно построить треугольник с катетами а и . затем из гипотенузы этого треугольника вычесть а/2 и оставшийся отрезок равный

отложим на первоначальном отрезке а (Рис. 1).

Если принять отрезок а за единичный, то получим следующее числовое выражение:

Число j – называется коэффициентом золотого сечения.

Мне кажется, я привела достаточно доказательств своей невинности.

Обвинитель. Господин судья, прошу слово.

Судья. Разрешаю.

Обвинитель. Допустим Вы везде по всюду, но какова же Ваша причастность к геометрии. Можете привести конкретный пример?

В защиту вызываются свидетели для решения этого вопроса.

Задача 1.

Построить правильный пятиугольник по данной стороне АВ = 1.

Решение:

Находим на отрезке АВ точку С золотого сечения. Из точки В как из центра проводим окружность радиусом АС, которая пересекает продолжение отрезка АВ в точке D.

Строим две окружности с центром А и В радиусом

AD = .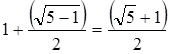

Одна из точек пересечения – точка Е, третья вершина пятиугольника. Потом из точки В чертим окружность радиусом АВ. Она пересекается с предыдущей окружностью в точке N, четвёртой вершине пятиугольника. Из точек А и Е проводим окружности, радиусы которых равны длине отрезка АВ (стороне правильного пятиугольника). Две последние окружности пересекаются в пятой вершине К пятиугольника.

Судья. Заседание продолжается. Слово предоставляется обвиняемой.

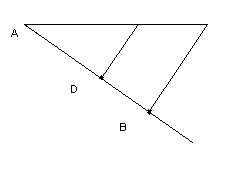
Обвиняемая. Что бы вспомнить меня надо проводить построения каждый раз. Что бы избежать этого воспользуемся теоремой Фалеса. Сначала вспомним, как она звучит: если параллельные прямые, пересекающие стороны угла, отсекают на другой его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Обвинитель. Протестую. Каким образом эта теорема причастна к делению отрезка на n равных частей, допустим на 3?

Обвиняемая. Давайте посмотрим на рисунок.

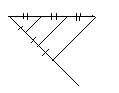
Возьмём теперь другой отрезок и разделим его в соответствии с золотым сечением, используя теорему Фалеса и отрезок, уже разделённый в золотом сечении. С этим отрезком поступим как и в предыдущем случае.

Судья. (Читает приговор). Именем Высших Адептов Света Великий Суд постановляет:

Статьи по педагогике:

Психолого-педагогическое обоснование исследуемой проблемы
Выбор средств обучения русскому языку, в том числе и средств развития речи школьников, опирается на достижения педагогики, дидактики, которая дает обобщенное понятие процесса обучения (это необходимо учителю). Успешное изучение русского языка невозможно без знания психологии обучаемых. Вот поэтому ...

Методика Дж. Холланда
Данный тест разработан для исследования профессиональных интересов и предпочтений человека. Он поможет соотнести склонности, способности и интересы с различными, конкретными профессиями, более точно определить круг запросов в профессиональной сфере и окажет содействие при планировании профессиональ ...

Практика дистанционного обучения
Одним из старейших университетов дистанционного обучения является University of South Africa, который начал предлагать курсы с 1946 года. Крупнейшим университетом дистанционного обучения считается британский Открытый университет, основанный в 1969 году. Немногим позже в 1974 году в Германии был осн ...